Ainda hoje em dia há gente que afirma que a evolução não é real e, o que é mais surpreendente, que a Terra é plana... com uma régua (veja vídeo no final do post). Guardando se as devidas proporções, o problema é o mesmo quando falamos com alguém sobre a dilatação do tempo em Relatividade Restrita ou de Física Quântica. De fato, foram necessários alguns para que os cientistas aceitassem a Deriva Continental que hoje aceitamos sem maior problema. Por que nos custa tanto crer em algumas destas coisas? Onde está o problema?

Esta reposta foi dada pelo genial Isaac Asimov: o problema é a precisão na medida. As teorias predizem os resultados de um experimento com maior ou menor exatidão e ser mais exatos nos permite conhecer detalhes que sem eles nossa concepção da Natureza seria totalmente diferente.

Tomemos, por exemplo, a Terra. Em nosso meio mais próximo vemos montanhas e vales, mas em geral, se não sairmos de dito meio, poderíamos aceitar que é plana e, de fato, os mapas que temos assim a consideram se o território compreendido não for muito grande.

Se realmente a Terra fosse plana, a curvatura seria absolutamente zero. Mas não é: a cada oito quilômetros o terreno declina cinco metros, o que corresponde a 0,625 metros por quilômetro. É um número muito pequeno, mas não é zero. A diferença entre o zero e esse número tem uma consequência decisiva: que a Terra não é plana.

Consideremos agora as Leis de Newton em frente à Relatividade de Einstein. A diferença, desta vez, está em que a luz demora em percorrer um metro 0,0000000033 segundos. A diferença entre esse número e 0 seria como considerar a velocidade da luz como infinita. E, realmente, a velocidade da luz é muito grande, mas não infinita. Se quisermos recuperar a teoria clássica e as transformações de Galileu a partir das transformações de Lorentz o único que há que fazer é mudar a velocidade da luz por infinito. Mas em nossa vida diária podemos fazer essa simplificação e considerar que faz um metro em zero segundos.

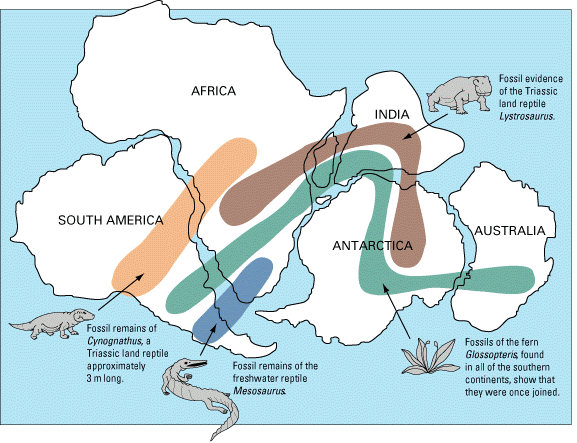
Outro exemplo está na deriva continental. Os continentes europeu e americano se afastam a razão de alguns poucos centímetros por ano. A diferença entre essa escassa distância e zero é a que coloca em marcha o processo da deriva continental. O mesmo acontece com as mutações na evolução. São processos tão lentos no tempo que mal são perceptíveis pelo homem (ainda que vejamos leigos argumentando que a evolução não existe porque não veem macaco virando gente hoje em dia. Aff!); mas não são exatamente zero, senão ligeiramente acima dele. É por isso que custou tanto para que estas teorias fossem aceitas.

O exemplo mais próximo e recente que temos é o caso das ondas gravitacionais. Conseguimos corroborar sua existência porque o Laser Interferometer Gravitational-Wave Observatory (LIGO) foi capaz de detectar estiramentos e compressões de 0,000000000000000001 metros em uma distância de 4 km. Só para que tenhamos uma ideia desse número, corresponde a milésima parte do diâmetro de um próton. A diferença entre um zero absoluto e essa mínima distância é a que nos permitiu corroborar que existem as ondas gravitacionais.

De modo que com estes exemplos já podemos ver a importância da precisão nas medidas: simplesmente podem mudar nossa visão da Natureza e do mundo que nos cerca.

Para provar a "teoria" da terra redonda, ficou faltando ligar a America do Sul tinha que estar ligada na Austrália ou India pelos fosseis.
A precisão na medida esta correta, teria que usar uma regua que é usada para medir planeza, contra a luz.

Por: Silas Siqueira 24 Fev, 2016 - 09:03:27